2016年電験1種　機械制御問3

電験1種 機械制御 電験

f:id:mahou:20190623223940j:plain

f:id:mahou:20190623223957j:plain

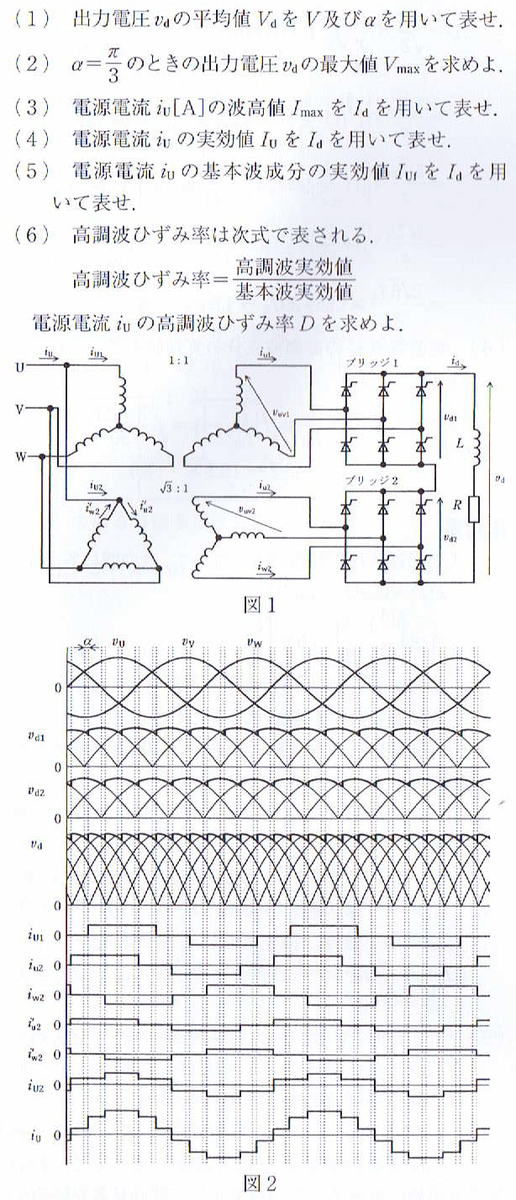
 (1)変圧器二次側の線間電圧実効値はVであるので、ブリッジ1の線間電圧を

v_\mathrm{uv1}=\sqrt{2}V \cos \theta

とすれば、v_\mathrm{d1}は60^\circごとの繰り返し波形で、 \displaystyle{\alpha-\frac{\pi}{6} \lt \theta \lt \alpha+\frac{\pi}{6}}の期間では、v_\mathrm{d1}=v_\mathrm{uv1}であるので、v_\mathrm{d1}の平均値は

\displaystyle{ V_\mathrm{d1}=\frac{3}{\pi}\int_{\alpha - \frac{\pi}{6}}^{\alpha + \frac{\pi}{6}} v_\mathrm{d1} d \theta = \frac{3\sqrt{2}V}{\pi}[\sin \theta]_{\alpha - \frac{\pi}{6}}^{\alpha + \frac{\pi}{6}}= \frac{3\sqrt{2}V}{\pi} \cos \alpha }

v_\mathrm{d1}と[tex:v_\mathrm{d2}の平均値は等しいので、

\displaystyle{V_\mathrm{d}= V_\mathrm{d1}+V_\mathrm{d2}= \frac{6\sqrt{2}V}{\pi}\cos \alpha}

 

(2)変圧器二次電圧の波高値は\sqrt{2}Vであり、Y-Y結線と\Delta -Y結線の変圧器の間には\displaystyle{30^\circ\left(\frac{\pi}{6} \mathrm{rad}\right)}の位相差があるので、制御角\alphaが\displaystyle{15^\circ\left(\frac{\pi}{12} \mathrm{rad}\right)}以下ではv_\mathrm{d}の最大値は、

\displaystyle{ \sqrt{2}V \times 2 \times \cos \frac{\pi}{12} = \sqrt{4+2\sqrt{3}}V}

である。制御角\alphaが15^\circ以上ではv_\mathrm{d}の最大値は余弦波状に低下する。したがって、\displaystyle{\alpha=\frac{\pi}{3}}のv_\mathrm{d}の最大値は、

\displaystyle{V_\mathrm{max}= \sqrt{4+2\sqrt{3}}V\cos\left(\frac{\pi}{3}-\frac{\pi}{12}\right) = \sqrt{4+2\sqrt{3}}V\cos \frac{\pi}{4} = \sqrt{2+\sqrt{3}}V}

なお、\alpha \gt 15^\circでは、転流直後の電圧が最大となるので、そのときの出力電圧の和から求めることもできる。

 

(3)変圧器二次電流の波高値は、すべてI_\mathrm{d}である。Y-Y結線変圧器の一次電流i_\mathrm{U1}は二次電流i_\mathrm{u1}に等しい。一方、巻数比を考慮すると、\Delta -Y結線変圧器の一次の巻線電流i'_\mathrm{u2},i'_\mathrm{w2}の波高値は\displaystyle{\frac{I_\mathrm{d}}{\sqrt{3}}}である。したがって、図2のように、一次電流i_\mathrm{U2}の波高値は\displaystyle{\frac{2}{\sqrt{3}}I_\mathrm{d}}である。したがって、電源電流i_\mathrm{U}の波高値は

\displaystyle{I_\mathrm{max}= I_\mathrm{d} + \frac{2}{\sqrt{3}}I_\mathrm{d} =\left( 1 + \frac{2}{\sqrt{3}} \right) I_\mathrm{d}}

 

(4)図2のように、電源電流i_\mathrm{U}は\displaystyle{\pm \frac{1}{\sqrt{3}}I_\mathrm{d}, \pm\left( 1 + \frac{1}{\sqrt{3}}\right) I_\mathrm{d}, \pm\left( 1 + \frac{2}{\sqrt{3}}\right)I_\mathrm{d}}の6値の繰り返し波形である。波形の対称性から、正の3値の二乗平均値の平方根（実効値）を求めると、

\displaystyle{I_\mathrm{U}= \sqrt{\frac{\left(\frac{1}{\sqrt{3}}\right)^2+\left(1+\frac{1}{\sqrt{3}}\right)^2+ \left(1+\frac{2}{\sqrt{3}}\right)^2}{3}} I_\mathrm{d} }

\displaystyle{= \sqrt{\frac{\frac{1}{3}+\left(1+\frac{2}{\sqrt{3}}+\frac{1}{3}\right)+ \left(1+\frac{4}{\sqrt{3}}+\frac{4}{3}\right)}{3}} I_\mathrm{d} = \sqrt{\frac{4+2\sqrt{3}}{3}} I_\mathrm{d} }

 

(5)基本波電流実効値をI_\mathrm{Uf}[\mathrm{A}]とすると、三相電源からの電力は抵抗Rの消費電力に等しいので、

\displaystyle{\sqrt{3}VI_\mathrm{Uf}\cos\alpha = V_\mathrm{d} I_\mathrm{d} = \frac{6\sqrt{2}VI_\mathrm{d}}{\pi}\cos\alpha}

となる。したがって、

\displaystyle{I_\mathrm{Uf} = \frac{2\sqrt{6}}{\pi} I_\mathrm{d}}

 

(6)高調波電流実効値は、\sqrt{ {I_\mathrm{U}}^2 - {I_\mathrm{Uf}}^2}であるので、高調波ひずみ率Dは、

\displaystyle{ D= \frac{\sqrt{ {I_\mathrm{U}}^2 - {I_\mathrm{Uf}}^2}}{I_\mathrm{Uf}} = \sqrt{\frac{{I_\mathrm{U}}^2}{{I_\mathrm{Uf}}^2}-1} = \sqrt{\frac{2+\sqrt{3}}{36}\pi^2 -1} }