根軌跡法2 - 数学・物理・電気主任技術者試験、情報処理技術者試験等お勉強の記録

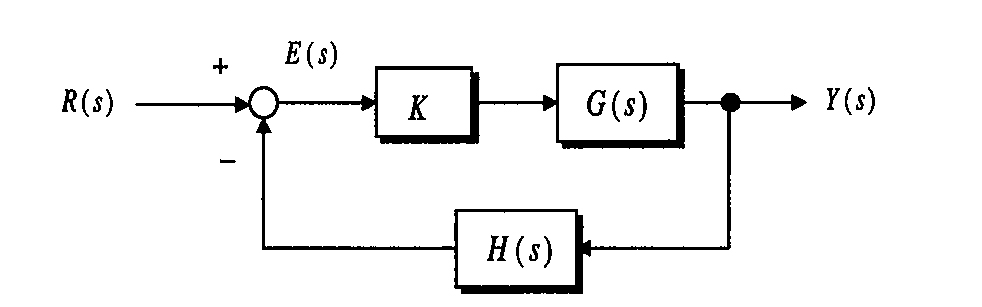
このブロック線図で表される制御系を考える。この制御系の特性方程式は

$1+KG(s)H(s)=0$

$s$ 平面上の任意の点が根軌跡上にあるための条件を求める。特性方程式は

$\displaystyle{1+KG(s)H(s)=1+ \frac{K \displaystyle{\prod_{j=1}^m} (s-z_i)}{\displaystyle{\prod_{i=1}^n} (s-p_i)} = 0}$

と一般に表される（ $G(s),H(s)$ の最高次の係数が1になるようにKをとれば一般性を失わない）。

$\displaystyle{KG(s)H(s)= \frac{K \displaystyle{\prod_{j=1}^m} (s-z_j)}{\displaystyle{\prod_{i=1}^n} (s-p_i)} = -1}$

より、

$\displaystyle{\frac{\displaystyle{\prod_{j=1}^m |s-z_j|}}{\displaystyle{\prod_{i=1}^n |s-p_i|}} = \frac{1}{K}}\tag{*}$

$\angle KG(s)H(s)= \sum_{j=1}^m \angle(s-z_j)-\sum_{i=1}^n \angle (s-p_i)=( 2 k +1 )\pi , k=0,\pm1,\pm2,\ldots$

【根軌跡の性質1】

$K=0$ を出発点とし $K=\infty$ を終点とする根軌跡は、(*)から $n$ 個の極を出発点とし、 $K=\infty$ なる点は $m$ 個の零点のいずれかだが、 $n-m$ 個は無限大に発散する。

【根軌跡の性質2】

無限遠に発散する $n-m$ 本の分岐はそれぞれある直線に漸近する。漸近線の角度は

$\displaystyle{\frac{(2k+1)\pi}{n-m}, k=0,1,2,\ldots}$

であり、漸近線と実軸との交点は

$\displaystyle{\frac{\displaystyle{\sum_{i=1}^n p_i - \sum_{j=1}^m z_j}}{n-m}}$

である。

$\displaystyle{ \frac{K \displaystyle{\prod_{j=1}^m} (s-z_j)}{\displaystyle{\prod_{i=1}^n} (s-p_i)} = -1}$

から $s$ が無限遠点に達したときには $|s|$ が非常に大きくなるので

$\displaystyle{\frac{s^n}{s^m} = -K}$

となるので、

$(n-m)\angle s = (2k+1)\pi$

一方、

$\displaystyle{ \frac{\displaystyle{\prod_{i=1}^n} (s-p_i)}{\displaystyle{\prod_{j=1}^m (s-z_j)}} = -K}$

$\displaystyle{-K=\frac{s^n -\displaystyle{\sum_{i=1}^n p_i} s^{n-1} + \cdots}{ s^m -\displaystyle{\sum_{j=1}^m z_i} s^{m-1} + \cdots} = s^{n-m} - \left(\sum_{i=1}^n p_i-\sum_{j=1}^m z_i\right)s^{n-m-1} + \cdots }$

ここで、 $s^{n-m-2}$ 以下のべき乗の項が $s^{n-m},s^{n-m-1}$ の項に比較して小さいことに注意すれば、

$\displaystyle{\left( s - \frac{\displaystyle{ \sum_{i=1}^n p_i-\sum_{j=1}^m z_j}}{n-m} \right)^{n-m} \Doteq -K}$

$n-m$ 個の解は

$\displaystyle{ s_k \Doteq K^{\frac{1}{n-m}} \exp\left( \sqrt{-1} \frac{2k+1}{n-m} \right) + \frac{\displaystyle{ \sum_{i=1}^n p_i-\sum_{j=1}^m z_j}}{n-m} }$

ゆえに漸近線と実軸との交点は

$\displaystyle{\frac{\displaystyle{ \sum_{i=1}^n p_i-\sum_{j=1}^m z_j}}{n-m}}$

【根軌跡の性質3】

根軌跡は実軸に関して対称である。

特性方程式は実方程式なので、実根か共役複素根のいずれかであるので、根軌跡は実軸に関して対称である。

【根軌跡の性質4】

実軸上に極や零点がいくつか存在する場合、それらの極と零点を区別せずにまとめて（重複極は重複度も数えて）右端の点から $P_1,P_2,\ldots$ と番号をつけるとき、奇数番目の点と偶数番目の点の間の線分 $[P_{2i-1},P_{2i}],i=1,2,\ldots$ は根軌跡の一部である。

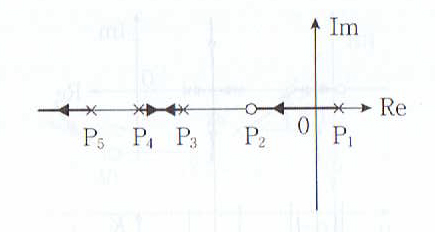
この性質は以下のようにして得られる。実軸上の任意の点 $s$ に対して位相条件を考える。

$\angle KG(s)H(s)= \sum_{j=1}^m \angle(s-z_j)-\sum_{i=1}^n \angle (s-p_i)=( 2 k +1 )\pi , k=0,\pm1,\pm2,\ldots$

実軸上にない極および零点はすべて複素共役な対からなるので、それらの偏角の和は0となり、互いに相殺する。したがって、実軸上の極および零点に対する位相条件のみを考慮すればよい。

点 $s$ の左側にある実軸上の極および零点に対する偏角は0、右側にあるそれらに対する偏角は $\pi$ である。よって点 $s$ の右側実軸上に合計奇数個の極および零点があればそれらの偏角の和は $\pi+2n\pi$ となるので、位相条件が満足される。すなわち線分 $[P_{2i-1},P_{2i}]$ 上の点 $s$ は根軌跡上にある。逆に線分 $[P_{2i-1},P_2i],i=1,2,\ldots$ 以外の実軸上の点 $s$ は位相条件を満たさない。

【根軌跡の性質5】

根軌跡が実軸上の線分から分岐（または合流）する場合

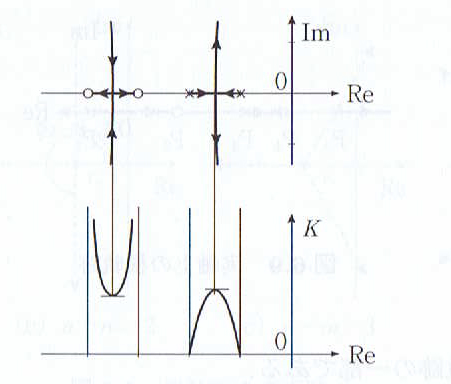
実軸上の根 $\sigma$ （実数）に対応するゲイン $\displaystyle{K(\sigma)= - \frac{1}{G(s)H(s)}}$ は分岐（または合流）点で極大（または極小）となる。ゆうに分岐（または合流）点の実軸座標 $\sigma_d$ は

$\displaystyle{\frac{d K(\sigma)}{d\sigma} =\frac{d}{d\sigma}\left(- \frac{1}{G(s)H(s)} \right) = 0 }$

を満たす。

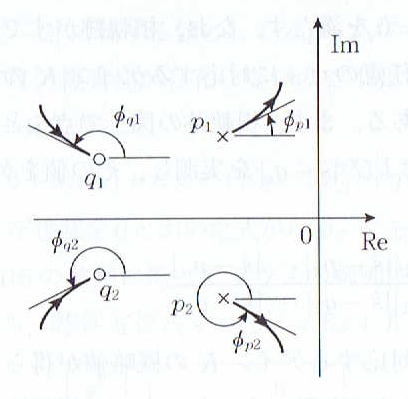
【根軌跡の性質6】

複素極 $p_j$ から根軌跡が出発する角度 $\phi_{pj}$ は

$\displaystyle{-\pi + \left[ \sum_{i=1}^m \angle (p_j -q_i) - \sum_{i=1(\ne j)}^n \angle(p_j-p_i) \right] \mod 2\pi}$

で与えられ、複素零点 $q_j$ に到達する角度 $\phi_{qj}$ は、

$\displaystyle{\pi - \left[ \sum_{i=1(\ne j)}^m \angle(q_j - q_i) - \sum_{i=1}^n \angle(q_j -p_i) \right] \mod 2\pi}$

で与えられる。

【根軌跡の性質7】

根軌跡が虚軸を横切る点の座標 $\omega_S$ とその時のゲインの値 $K_S$ は[1+K_S G(\sqrt{-1}\omega_s)=0]を満たす $\omega_S$ と $K_S$ として得られる。なお、Routh（Hurwitz）の判別法法を用いて安定限界のゲイン $K_S$ を求めてもよい。

虚軸上の点は $s=\sqrt{-1}\omega$ と表され、虚軸と根軌跡の交点は $1+KG(\sqrt{-1}\omega)H(\sqrt{-1}\omega)=0$ を満たす。なお、根軌跡がすでに得られている場合に、その根軌跡上の任意の点 $\hat{s}$ に対応するゲイン $K$ の概略値をしりたい時には、以下の方法がある。まず、根軌跡の図上で点 $\hat{s}$ と全ての極および零点の間の距離 $|\hat{s}-p_i|$ および $|\hat{s}-q_i|$ を実測し、その値をゲイン条件